Dalam matematika, segitiga Pascal adalah suatu aturan geometri pada koefisien binomial dalam sebuah segitiga. Ia dinamakan sempena Blaise Pascal dalam kebanyakan dunia barat, meskipun ahli matematika lain telah mengkajinya berabad-abad sebelum dia di India, Persia, Cina, dan Italia. Barisan segitiga Pascal umumnya dihitung dimulai dengan baris kosong, dan nomor-nomor dalam barisan ganjil biasanya diatur agar terkait dengan nomor-nomor dalam baris genap. Konstruksi sederhana pada segitiga dilakukan dengan cara berikut. Di barisan nol, hanya tulis nomor 1. Kemudian, untuk membangun unsur-unsur barisan berikutnya, tambahkan nomor di atas dan di kiri dengan nomor secara langsung di atas dan di kanan untuk menemukan nilai baru. Jika nomor di kanan atau kiri tidak ada, gantikan suatu kosong pada tempatnya. Misalnya, nomor satu di barisan pertama adalah 0 + 1 = 1, di mana nomor 1 dan 3 dalam barisan ketiga ditambahkan untuk menghasilkan nomor 4 dalam barisan keempat.
Pembinaan ini terkait dengan koefisien binomial oleh Peraturan Pascal, yang menyatakan bahwa jika
adalah koefisien binomial ke-'k dalam pengembangan binomial pada (x + y)n, di mana n! adalah faktorial n, oleh itu
untuk setiap bilangan bulat bukan negatif n dan mana-mana bilangan bulat k di antara 0 dann.[1]
Segitiga Pascal memiliki pengitlakan dimensi lebih tinggi. Versi tiga-dimensi disebutPiramida Pascal atau Pascal 's tetrahedron, sedangkan versi umum disebut simpleks Pascal - ini lihat piramida, tetrahedron dan simpleks.
[sunting]Segi tiganya
Di bawah adalah barisan kosong ke enam belas pada segitiga Pascal:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
1 11 55 165 330 462 462 330 165 55 11 1
1 12 66 220 495 792 924 792 495 220 66 12 1
1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1
1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1
1 15 105 455 1365 3003 5005 6435 6435 5005 3003 1365 455 105 15 1
1 16 120 560 1820 4368 8008 11440 12870 11440 8008 4368 1820 560 120 16 1
[sunting]Segi tiga Pascal dan pengembangan binomial
Segi tiga Pascal menentukan koefisien yang menambahkan dalam pengembangan binomial. Misalnya, timbangkan pengembangan berikutnya.
- (x + y)2 = x2 + 2xy + y2 = 1x2y0 + 2x1y1 + 1x0y2.
Perhatikan bahwa koefisien adalah angka dalam baris kedua segitiga Pascal: 1, 2, 1. Pada umumnya, ketika sebuah binomial seperti x+ y ditambahkan ke suatu bilangan bulat positif kita mendapat:
- (x + y)n = a0xn + a1xn−1y + a2xn−2y2 + … + an−1xyn−1 + anyn,
yaitu koefisien ai dalam pengembangan ini adalah tepatnya bilangan dalam baris n segitiga Pascal '. maknanya,
Ini adalah teorema binomial.
Perhatikan bahwa keseluruhan diagonal kanan segitiga Pascal berhubungan dengan koefisien yn dalam pengembangan binomial ini, sedangkan diagonal berikutnya berhubungan dengan koefisien xyn-1 dan sebagainya.
Untuk melihat bagaimana teorema binomial terkait dengan konstruksi sederhana segitiga Pascal, pertimbangkan masalah perhitungan koefisien pengembangan (x + 1)n+1 dari segi koefisien yang berhubungan (x + 1)n (letakkan y = 1 untuk lebih mudah). Anggap setelah itu bahwa
Sekarang
Dua penjumlahan dapat diatur kembali sebagai berikut:
(karena cara penambahan suatu polinomial ke suatu kekuasaan berhasil, a0 = an = 1).
Kita sekarang memiliki pernyataan untuk polinomial (x + 1)n+1 dari segi koefisien (x + 1)n (ini adalah ais), yaitu kita perlu jika ingin menyatakan suatu baris dari kiri-atas ke kanan-bawah berkoresponden dengan energi yang sama x, dan bahwa jangka-a adalah koefisien polinomial (x + 1)n, dan kita menentukan koefisien (x + 1)n+1. sekarang, untuk mana-mana i diberikan bukan 0 atau n + 1, pekali jangka xi dalam polinomial (x + 1)n+1 adalah bersamaan dengan ai (tokoh di atas dan di kanan tokoh untuk ditentukan, sejak ia adalah pada pepenjuru yang sama) + ai−1 (tokoh di kanan secara terus pada tokoh pertama). Ini sudah tentu peraturan mudah untuk pembinaan segitiga Pascal baris-demi-baris.
Adalah tidak susah untuk mengitarkan perdebatan ini ke dalam bukti (oleh induksi matematik) pada teorem binomial.
Suatu akibat menarik pada teorem binomial didapatkan dengan memuatkan dua jenis x dan y bersamaan dengan satu. Dalam kes ini, kita tahu bahawa  , dan oleh itu
, dan oleh itu
 , dan oleh itu
, dan oleh itu
Maknanya, jumlah kemasukan pada baris ke-n pada segitiga Pascal adalah tenaga ke-n pada 2.
[sunting]Referensi
- ^ Pekali binomial
 adalah secara kebiasaan diletakkan kosong jika k sama ada kurang daripada kosong atau lebih besar daripadan.
adalah secara kebiasaan diletakkan kosong jika k sama ada kurang daripada kosong atau lebih besar daripadan.

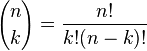

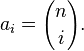









0 komentar:
Posting Komentar