Relasi

Relasi, dalam matematika, adalah hubungan antara dua elemen himpunan. Hubungan ini bersifat abstrak, dan tidak perlu memiliki arti apapun baik secara konkrit maupun secara matematis.

DEFINISI

Jika terdapat himpunan A dan himpunan B (A bisa sama dengan B), maka relasi R dari Ake B adalah subhimpunan dari A×B.

RELASI DAN FUNGSI PROPOSISI

Sebuah relasi dapat dikaitkan dengan sebuah fungsi proposisi atau kalimat terbuka yang himpunan penyelesaiannya tidak lain adalah relasi tersebut.
Sebagai contoh, pandang himpunan B = { apel, jeruk, mangga, pisang } dengan himpunan W = { hijau, kuning, orange}. Suatu relasi R dari A ke B didefinisikan sebagai R= {(apel, hijau), (jeruk, orange), (mangga, hijau), (pisang, kuning)}. Terdapat fungsi proposisi w(x, y) = "x berwarna y", yang himpunan penyelesaiannya adalah {(apel, hijau), (jeruk, orange), (mangga, hijau), (pisang, kuning)}, yang tidak lain adalah relasi R.

RELASI A×A

Sebuah relasi A×A, yaitu relasi dari himpunan A kepada A sendiri, dapat memiliki sifat-sifat berikut:

Refleksif
Irefleksif
Simetrik
Anti-simetrik
Transitif

Kita menyebut relasi R dari A kepada A sebagai relasi R dalam A.

Relasi Refleksif

Sebuah relasi R dalam A disebut memiliki sifat refleksif, jika setiap elemen Aberhubungan dengan dirinya sendiri.

$\forall_{a \in A}\quad (a,a) \in R$

atau

$\forall_{a \in A}\quad a R a$

Contoh relasi yang memiliki sifat seperti ini adalah relasi “x selalu bersama y.”, dengan xdan y adalah anggota himpunan seluruh manusia. Jelas sekali bahwa setiap orang pasti selalu bersama dengan dirinya sendiri.

Relasi Irefleksif

Relasi R dalam A disebut memiliki sifat irefleksif, jika setiap elemen A tidak berhubungan dengan dirinya sendiri.

$\forall_{a \in A}\quad (a,a) \notin R$

atau

$\forall_{a \in A}\quad \lnot(a R a)$

Contoh relasi irefleksif adalah relasi “x mampu mencukur rambut y dengan rapi sempurna.”, dengan x dan y adalah setiap pemotong rambut. Diandaikan bahwa setiap orang hanya dapat mencukur rambut orang lain dengan rapi sempurna, maka relasi ini adalah irefleksif, karena tidak ada seorang tukang cukur a yang mampu mencukur rambutnya sendiri.
Contoh lain dalam himpunan bilangan bulat adalah, relasi < dan > adalah irefleksif.

Relasi Simetrik

Relasi R dalam A disebut memiliki sifat simetrik, jika setiap pasangan anggota Aberhubungan satu sama lain. Dengan kata lain, jika a terhubung dengan b, maka b juga terhubung dengan a. Jadi terdapat hubungan timbal balik.

$\forall_{a, b \in A}\quad (a,b) \in R \rightarrow (b,a) \in R$

atau

$\forall_{a, b \in A}\quad a R b \rightarrow b R a$

Sebuah relasi “

x + y

genap” adalah relasi simetrik, karena untuk sembarang x dan y yang kita pilih, jika memenuhi relasi tersebut, maka dengan menukarkan nilai y dan x, relasi tersebut tetap dipenuhi. Misalnya untuk pasangan (5, 3) relasi tersebut dipenuhi, dan untuk (3, 5) juga.

Relasi Anti-simetrik

Jika setiap a dan b yang terhubung hanya terhubung salah satunya saja (dengan asumsia dan b berlainan), maka relasi macam ini disebut relasi anti-simetrik.

$\forall_{a, b \in A}\quad a \neq b \rightarrow ((a,b) \in R \rightarrow (b,a) \notin R)$

atau

$\forall_{a, b \in A}\quad a \neq b \rightarrow (a R b \rightarrow \lnot (b R a))$

Dalam kebanyakan literatur biasanya ditulis sebagai kontraposisinya seperti di bawah ini. Keuntungan bentuk ini adalah tidak mengandung negasi, dan hanya mengandung satu implikasi.

$\forall_{a, b \in A}\quad (a,b) \in R \wedge (b,a) \in R \rightarrow a=b$

atau

$\forall_{a, b \in A}\quad a R b \wedge b R a \rightarrow a=b$

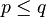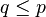Relasi $\leq$ bersifat anti-simetrik, karena $5 \leq 6$ mengakibatkan $\lnot (6 \leq 5)$ . Demikian juga jika ada p dan q yang terhadap mereka berlaku $p \leq q$ dan $q \leq p$ berarti

p = q

Relasi Transitif

Sebuah relasi disebut transitif jika memiliki sifat, jika a berhubungan dengan b, dan bberhubungan dengan c, maka a berhubungan dengan c secara langsung.

$(a,b) \in R \wedge (b,c) \in R \rightarrow (a,c) \in R$

atau

$\forall_{a, b, c \in A} {a R b \wedge b R c \rightarrow a R c}$

Sebagai contoh, relasi dua transitif. Misalnya untuk 5, 6, dan 7, berlaku 5 < 6, 6 < 7, dan 5 < 7.

RELASI KHUSUS

Relasi Ekivalen

Sebuah relasi disebut sebagai relasi ekivalen jika relasi tersebut bersifat:

Refleksif
Simetrik, dan
Transitif

Relasi ekuivalen memiliki hubungan erat dengan partisi, yang merupakan alasan mengapa partisi dari sebuah himpunan disebut kelas ekivalen atau kelas kesetaraan.

Orde Parsial

Orde parsial adalah relasi yang bersifat:

Refleksif
Anti-simetrik, dan
Transitif

Fungsi (matematika)

Fungsi, dalam istilah matematika adalah pemetaan setiap anggota sebuah himpunan(dinamakan sebagai domain) kepada anggota himpunan yang lain (dinamakan sebagaikodomain). Istilah ini berbeda pengertiannya dengan kata yang sama yang dipakai sehari-hari, seperti “alatnya berfungsi dengan baik.” Konsep fungsi adalah salah satu konsep dasar dari matematika dan setiap ilmu kuantitatif. Istilah "fungsi", "pemetaan", "peta", "transformasi", dan "operator" biasanya dipakai secara sinonim.
Anggota himpunan yang dipetakan dapat berupa apa saja (kata, orang, atau objek lain), namun biasanya yang dibahas adalah besaran matematika seperti bilangan riil. Contoh sebuah fungsi dengan domain dan kodomain himpunan bilangan riil adalah y=f(2x), yang menghubungkan suatu bilangan riil dengan bilangan riil lain yang dua kali lebih besar. Dalam hal ini kita dapat menulis f(5)=10

NOTASI

Untuk mendefinisikan fungsi dapat digunakan notasi berikut.

$f : A \rightarrow B$

Dengan demikian kita telah mendefinisikan fungsi f yang memetakan setiap elemen himpunan A kepada B. Notasi ini hanya mengatakan bahwa ada sebuah fungsi f yang memetakan dua himpunan, A kepada B. Tetapi bagaimana tepatnya pemetaan tersebut tidaklah terungkapkan dengan baik. Maka kita dapat menggunakan notasi lain.

$x \in A$

$f : x \rightarrow x^2$

atau

FUNGSI SEBAGAI RELASI

Sebuah fungsi f dapat dimengerti sebagai relasi antara dua himpunan, dengan unsur pertama hanya dipakai sekali dalam relasi tersebut.

DOMAIN DAN KODOMAIN

Domain adalah daerah asal, kodomain adalah daerah kawan, sedangkan range adalah daerah hasi

Relasi

Relasi, dalam matematika, adalah hubungan antara dua elemen himpunan. Hubungan ini bersifat abstrak, dan tidak perlu memiliki arti apapun baik secara konkrit maupun secara matematis.

DEFINISI

Jika terdapat himpunan A dan himpunan B (A bisa sama dengan B), maka relasi R dari Ake B adalah subhimpunan dari A×B.

RELASI DAN FUNGSI PROPOSISI